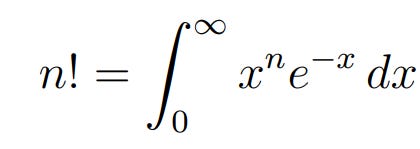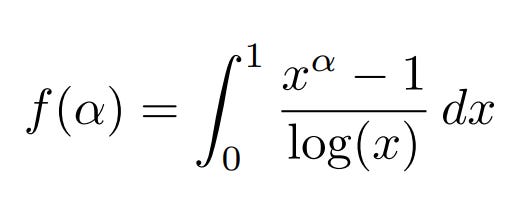How To Integrate Using Feynman's technique

Mastering Integration: A Practical Guide Through Feynman's Technique

Professor Feynman:

‘One thing I never did learn was contour integration. I had learned to do integrals by various methods show in a book that my high school physics teacher Mr. Bader had given me. The book also showed how to differentiate parameters under the integral sign - It’s a certain operation. It turns out that’s not taught very much in the universities; they don’t emphasize it. But I caught on how to use that method, and I used that one damn tool again and again. So because I was self-taught using that book, I had peculiar methods of doing integrals. The result was that, when guys at MIT or Princeton had trouble doing a certain integral, it was because they couldn’t do it with the standard methods they had learned in school. If it was contour integration, they would have found it; if it was a simple series expansion, they would have found it. Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else’s, and they had tried all their tools on it before giving the problem to me.’

The "Feynman Integration" method is a straightforward implementation of a theorem credited to Leibniz. Our focus is on scenarios where we aspire for the validity of the following equation:

Before stating these theorems, recall that differentiation is simply a particular example of a limit insofar as we define:

with a true definition on the far right. Thus, we see that (2) will hold whenever we may make the following statement:

Derivation Of The Gamma Function

A historical challenge involves extending the factorial function to non-integer values. Euler successfully addressed this problem by uncovering two formulas for n!—one expressed as an integral and the other as an infinite product.

Let,

The integral is easily evaluated: F(t) = 1 t for all t > 0. Differentiating F with respect to t leads to the identity:

Taking further derivatives yields:

Which immediately implies the formula:

The right hand side is the famous Gamma function, and does not depend on n being an integer.

This example captures the spirit of Feynman’s trick: when integrating a function with respect to one variable, one can differentiate with respect to a different variable and sometimes glean new information.

Another Example To Demonstrate Feynman’s Technique

To evaluate:

First, introduce a parameter, say α, into the integral, thereby creating a function of this parameter.

The problem now is to find f(5). This will be done by computing f’(α)—taking the derivative with respect to α inside the integral—then integrating with respect to x to get an explicit expression for f’(α). Finally, integrating this expression with respect to α gives an expression for f(α):

Now integrating with respect to α gives

Since f(0) = 0, we see that c = 0 and f(α) = log(α+ 1). The answer to our original problem is then f(5) = log(6). In fact, we have derived the general formula:

In essence, Feynman's integration technique involves rewriting an integral in a more accessible form by introducing an auxiliary parameter and then differentiating with respect to that parameter. This process allows for a strategic manipulation of the integrand, often leading to a more manageable expression that can be readily solved. Really, the beauty of Feynman's trick lies in its versatility…