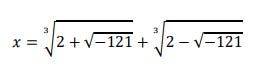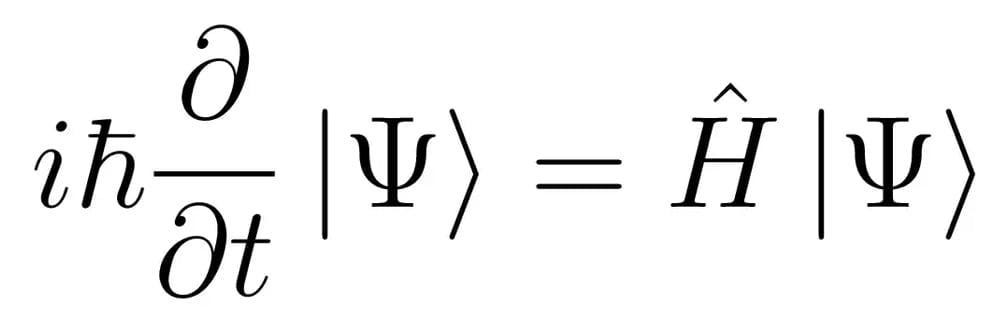Why Does 'i' Appear In Schrödinger's equation? - A Comprehensive Guide To ℂomplex Numbers

"Unlocking the World of ℂomplex Numbers: A Thorough Guide to Understanding and Mastering Their Mathematics

You encountered numbers at such an early stage in your academic journey that by now, you likely view them as an inherent part of the natural order—entities seamlessly integrated into the fabric of mathematical concepts. This perception underscores the potency of early indoctrination, despite the fact that the reality is quite distinct. The positive integers, those used for counting, are inherently natural, while the remaining numbers are human inventions devised to facilitate problem-solving in mathematics. Consequently, the concept of "number" has evolved significantly over the centuries.

If you were to journey back to the sixteenth century and consult the era's mathematics professor with the equation x^2 + x = 6, you'd receive the response that x equals 2. However, tackling the problem today would yield two solutions: x = 2 and x = −3. The disparity doesn't stem from a variance in skill or diligence but rather from a difference in perspective. In the sixteenth-century European mathematical mindset, numbers were tools for counting and measuring; the concept of negative oranges, lengths, or areas was nonexistent, and consequently, negative numbers were not acknowledged. While some mathematicians were daring enough to manipulate negative quantities in addition and subtraction, accepting negative solutions was beyond their willingness. This perspective isn't illogical; it's a matter of viewpoint. Going further back, you'd encounter a time when zero didn't exist as a number. Again, this absence wasn't illogical; it simply reflected a lack of perceived necessity, as people hadn't recognised the need for such a number. Notions evolve as individuals realise that old perspectives are insufficient for their evolving needs.

By the seventeenth century, the utility of manipulating negative quantities was prompting a significant shift in perspective. The concept of the real number line emerged, placing positive numbers to the right of zero and negative ones to the left. While interpretations involving credit and debt contributed to this shift, negative numbers still did not enjoy the same status as their positive counterparts. Even in the eighteenth century, some writers resisted the notion of multiplying two negative numbers together, deeming it too paradoxical to accept, despite the sensibility of positive times negative in the context of directed distances on the real line. Nowadays, such concerns have dissipated. The consensus is that mathematics is more manageable and convenient with the inclusion of negative numbers, leading to their widespread acceptance. Thankfully, various methods have been devised to provide them with a solid, logical foundation.

Ok, let’s go back to our sixteenth-century mathematician and ask him to solve these equations:

The initial equation is quadratic, and the method for solving such equations has been known since the time of the Babylonians around 2000 B.C. When applied, it yields solutions in the form of x = ± 1, leading our mathematician to declare that the equation has no solution. This conclusion, likely echoed in your school education, is entirely logical, akin to the denial of negative numbers. There is no apparent reason to adopt a different perspective in this case.

HOWEVER: the second equation would have piqued more interest. The first significant mathematical breakthrough of the European Renaissance involved solving cubic equations. While the method is intricate and often omitted from educational curricula due to its complexity, it does exist. Applied to this equation, it unveils the answer...

At first glance, this appears like rubbish, leading to the initial assumption that it is another equation with no solution. However, upon closer inspection, it becomes evident that the equation does indeed have a solution: x = 4. Thus, in some way, the right hand side must equal 4.

Inspired by this curiosity, individuals began exploring the concept of square roots of negative numbers to see what possibilities might unfold if such entities were to exist. They didn't assert that their endeavors were inherently meaningful; rather, the exploration was driven by a sense of curiosity and the realization that the results obtained did, surprisingly, align with correctness. Initially dismissed as fanciful and improbable, this observation experienced a resurgence when Leibniz revisited the idea in the late 17th century. From that point until around 1800, it gained increasing importance as a tool for uncovering results that could then be validated through more conventional methods. This was the trajectory of "imaginary numbers" in the 18th century.

Now, here’s what Leonhard Euler (the greatest mathematician of all time?) had to say in his book ‘elements of algebra’:

So, a complex number is any number that can be written as a+bi, where i is the imaginary unit and a and b are real numbers.

a is called the real part of the number, and b is called the imaginary part of the number.

Remember:

i = √-1

i^2 = -1

Now, we can plot real numbers, but what about complex numbers? Of course we can plot them!

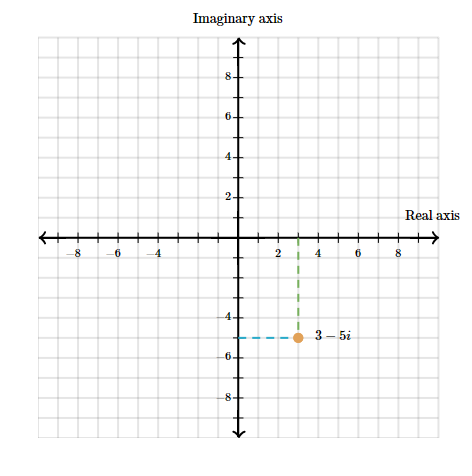
The complex plane is formed by the intersection of two number lines at a right angle, pinpointed at the origin (0,0). The first of these lines, extending horizontally and corresponding to the familiar x-axis in a Cartesian plane, is referred to as the real axis. Simultaneously, the second line, extending vertically and representing the conventional y-axis in a Cartesian plane, is termed the imaginary axis.

Plotting Complex numbers:

When plotting a complex number, every such number finds its representation as a point in the complex plane. Take, for instance, the number 3−5i, which can also be expressed as 3+(−5)i. Here, 3 denotes the real part, and −5 represents the imaginary part. This number is located on the complex plane at the point corresponding to 3 on the real axis and −5 on the imaginary axis.

Ok, now where else do complex numbers show up in the world? Well, ever heard of the Schrödinger equation?

Upon first inspection, to most readers this will mean nothing. And you don’t need to fully understand this equation to realise the importance of the first term ‘i’. What’s that? Our imaginary number…

The Schrödinger equation tells you how a state evolves with time. Suppose the system is at t=0 in a normalised eigenstate ψ(0) of the Hamiltonian with eigenvalue E. Because the Hamiltonian is an hermitian operator we know that E is real. To obtain the time evolution you must solve the equation.

Eψ=i∂tψ

Don’t worry about this step, I’ll do it for you.

which gives ψ(t)=e^−iEt * ψ(0). Just know that, |ψ(t)|=|ψ(0)|=1, satisfying the rule that the sum of all the probabilities must be equal to one. This is called unitarity.

If the imaginary unit i wasn't there, the solutions would be ψ(t)=e^Et * ψ(0), and we wouldn't have constant |ψ(t)| breaking this basic principle.

Effectively, complex numbers have an amplitude and phase. The i is one way of describing the phase. Wave-functions just map a coordinate to a complex number, from which you can get the amplitude and phase of a wave. Phase is what allows interference in Quantum Mechanics. In a classical description of the two slit interferometer you'd have real amplitudes going through each, no phase or interference

Now, you fully understand Complex numbers.